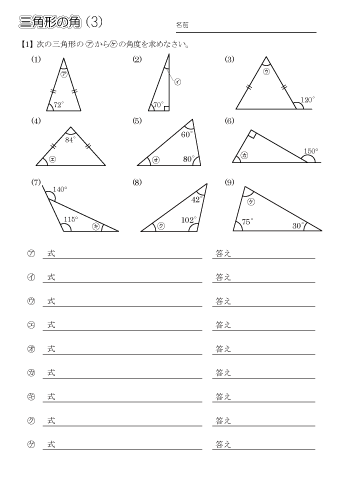
・二等辺三角形では、3つの角度のうち1つが分かれば残りの角度も計算できます。 ・計算には、 頂角 + 底角 + 底角 =180° という関係を使います。 ・(おまけ) 下の図のように二等辺三角形の向きが変わっても、頂角と底角を間違えないようにしましょう。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75°角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。

解答 オリジナル問題2 2つの辺の長さが同じ三角形 図形問題で柔らか頭に 算数オリピック 中学入試問題にチャレンジ
三角形の角度は
三角形の角度は- まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °



三角形の中の角度
正三角形の角度問題 まとめ お疲れ様でした! 正三角形の性質としては このように単純な性質しかないので 問題としては、いろんな図形との融合で出題されがちです。 正三角形どうしの融合の場合 60°の角になるところをしっかりと見つけていくこと 3 三角形の内角の和が180°であることから角度Cを求める。 4 正弦定理を用い,辺cを求める。 ハッキリ言って6つの組がすべて求められるのは三角定規のような三角形に限られるといっても過言ではなく,一部だけわかるということも多いです。・直角三角形(高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。 ・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数
三角比として頻繁にでてくる角度は、 30度と45度と60度 です。 中学生では、この3つの角度の時の三角形の比率を全て覚えておけば、数学の三角図形の問題はなんとか乗り越えられます。三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺
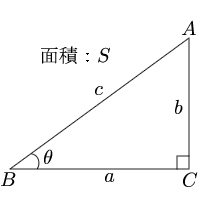
角度の計算基本プリントと少し難易度が高い良く出るプリント集を掲載しています 小学5年生で習う三角形の角度計算です 4年で習うより少し複雑です それ以外にも、三角形の角度計算で覚えなければならない決まり事も掲載しています三角形计算器 如果给出足够的几何属性, 任意三角形计算器 就能自动补全任意三角形的所有属性,例如面积,周长,边和角度。 三角形是具有三个顶点(角)和三条边(边)的多边形。 任意三角形 维基百まずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみま



直角三角形 底辺と角度 三角形の計算 計算サイト
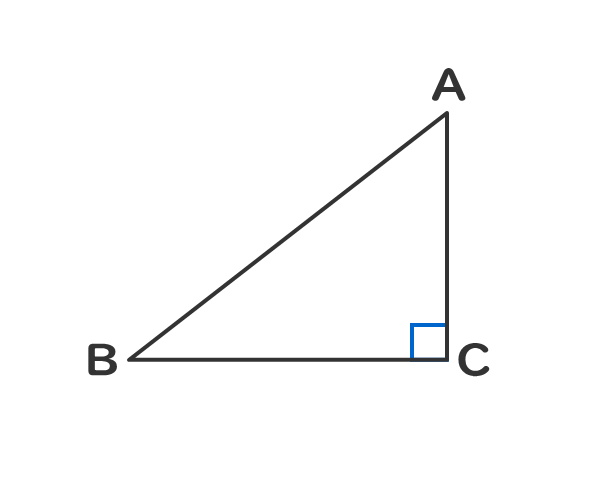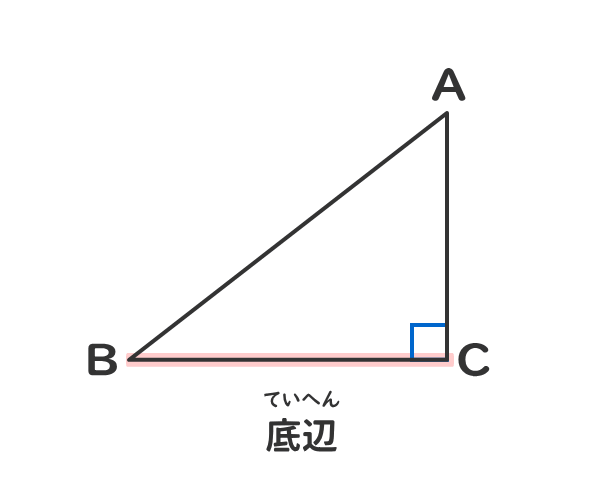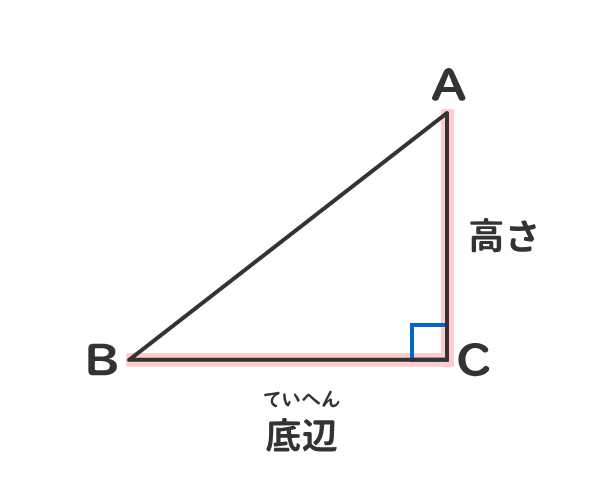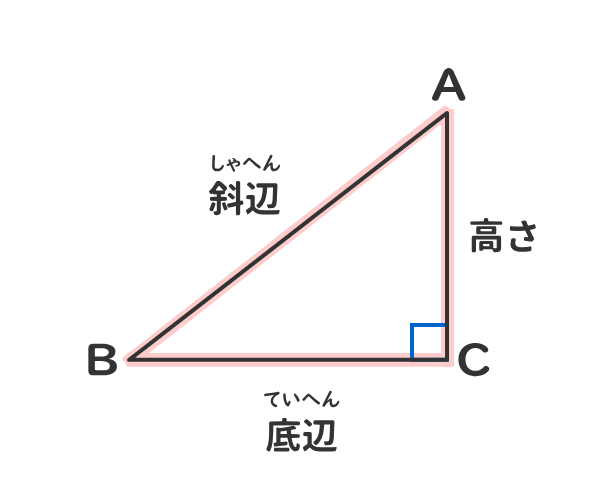



二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web
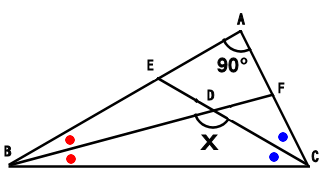
小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。角度の難問 (中学生版) 1 /32 問題 AB=ACの二等辺三角形 ABC があり,角Aは ° です。 いま,辺 AC 上に点D,辺 AB 上に点Eがあり,DからB,EからCに直線を引いたところ,角 DBC = 60° ,角 ECB = 50° となりました。 DからEまで直線を引いたとき,角 BDE (図のχ 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な
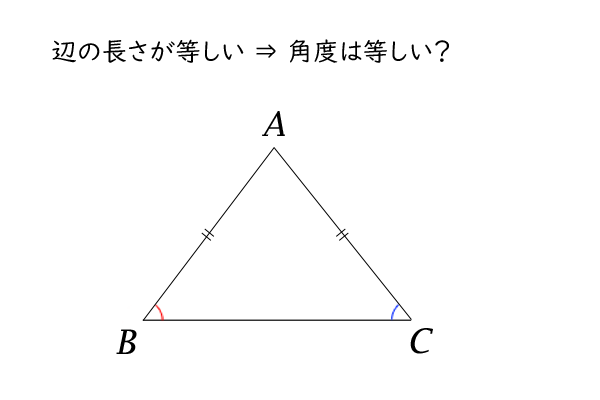



三角形の辺の長さと角の大きさの関係 高校数学マスター




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
三角形の内角と外角の関係から ● = ○ + ● 角A=30°+90°=1° 三角形とは、 同一直線上にない 点と、それらを結ぶ つの線分からなる多角形 です。まとめ 三角形の3つの内角をくっ付けて並べると、直線になります。 直線の角度は180°なので、三角形の内角の和は180°になります。 いかがでしたか? 三角形の内角の和が何度だったか忘れてしまったときにも、ぜひ参考にして下さい。 この公式を使っ




直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe




三角形の中の角度
直角三角形计算 直角三角形在线计算器 请在下面输入数值 (图形在下面) a垂直边长 b底边长 c斜边长 A角度 B角度 C角度 解説&答えはこちら 答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺 (1)三角形内角和:A+B+C=π。 (2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等, a/sinA=b/sinB=c/sinC=2R(R为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍
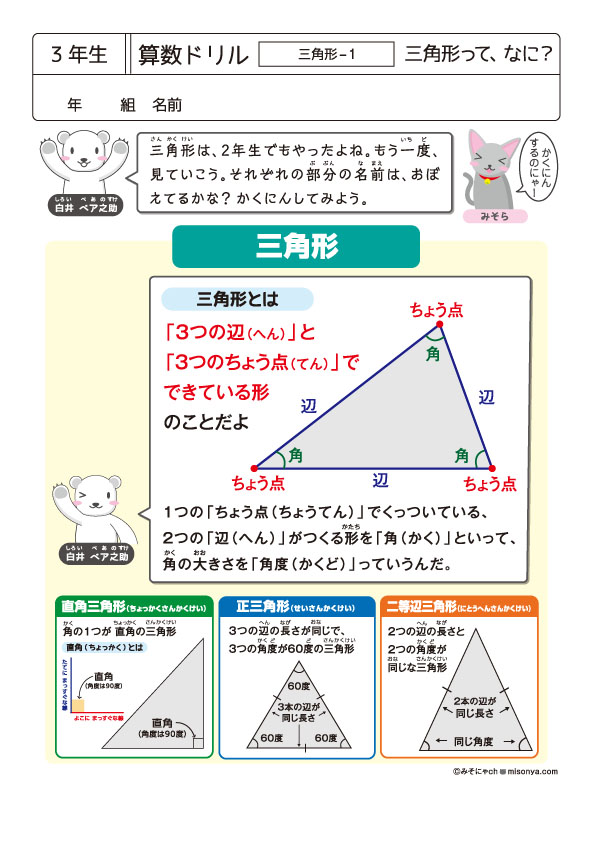



無料の学習プリント 小学3年生の算数ドリル 三角形 みそにゃch
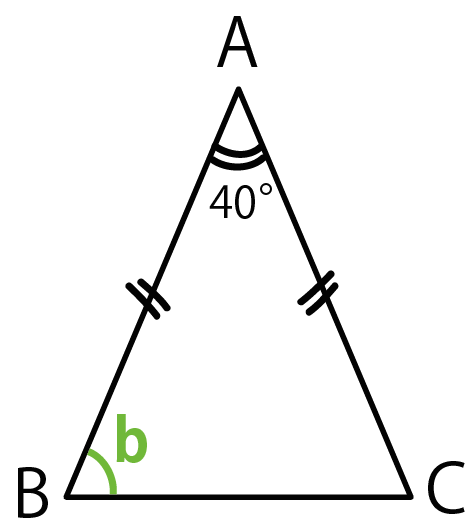



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく
直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った / 辺 a辺 b辺 c - 辺 b辺 c - 計 算クリア 角度 θ 度 スポンサードリンク <参考記事> 三角関数の計算 度⇔ラジアン 単位変換 最終更新 18年5月24日二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底



三角形の角度から分かる 宇宙の形 とは Gigazine




二等辺三角形の角度 無料で使える中学学習プリント
計算問題も徹底解説 21年2月19日 この記事では、三角関数について、角度の求め方や変換公式( など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね! 目次 非表示 三角関数の二等辺三角形の角度は? 二等辺三角形の角度は、1つの角度が分かれば、他の2つの角度が計算できます。下図をみてください。これが二等辺三角形です。 三角形の角度は合計すると180度です。頂角をα、低角をθとします。よって α2θ=180 です。三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。



1




タンジェントとは何か 中学生でも分かる三角関数の基礎
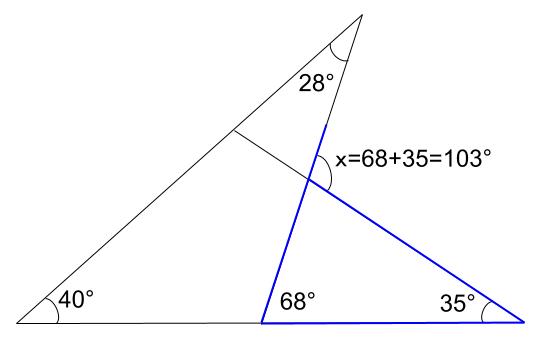
星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して 已知三角形边长,计算三角形的角度过程如下: 1、设三角形中角A所对应的边长是a,角B所对应的边长是b,角C所对应的边长是c。 再利用公式: ①CosA= (c^2b^2a^2)/2bc ②CosB= (a^2c^2b^2)/2ac ③CosC= (a^2b^2c^2)/2ab 算出每一个角的余弦值,利用计算器上的反余弦函数 二等辺三角形の角度の求め方がわかる2つの公式 二等辺三角形の角度は2パターンで計算できちゃうよ。 頂角から底角を求めるパターン 底角から頂角を求めるパターン 順番に紹介していくよー! ! パターン1 頂角がわかっている問題 まずは、
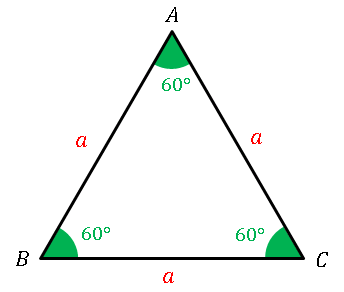



正三角形の性質 角度 面積 周の長さ 対称性



三角形の角度を求める問題がわかりません 三角形の和と直線の角度 Yahoo 知恵袋
/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e (1) cos 求めることができる角度はコレ↓↓ 三角形の外角と内角の関係から、 55°30=∠x よって∠x=85° ・・・(答え) 問題③ こいつも一筋縄ではいかねーな! 右側の三角形で、三角形の外角と内角の関係を利用しよう。 65°45°=110° 次に、左の三角形に着目四 、用计算器的 tan1 键来求角度 Tan x° = 对边/邻边 = 300/400 = 075 tan1 of 075 = 369° (保留一位小数)
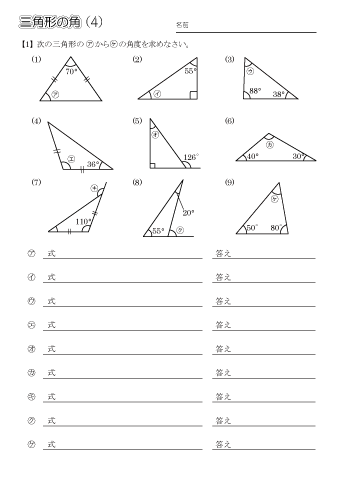



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角形の角度を求める問題 小学生 中学生の勉強
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
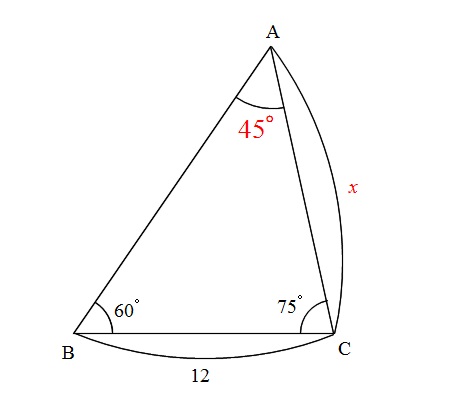



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



三角形とは コトバンク
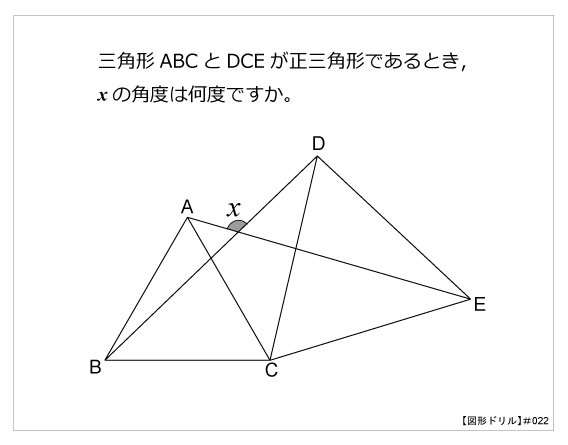



図形ドリル 第22問 正三角形の回転合同 算数星人のweb問題集 中学受験算数の問題に挑戦



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明
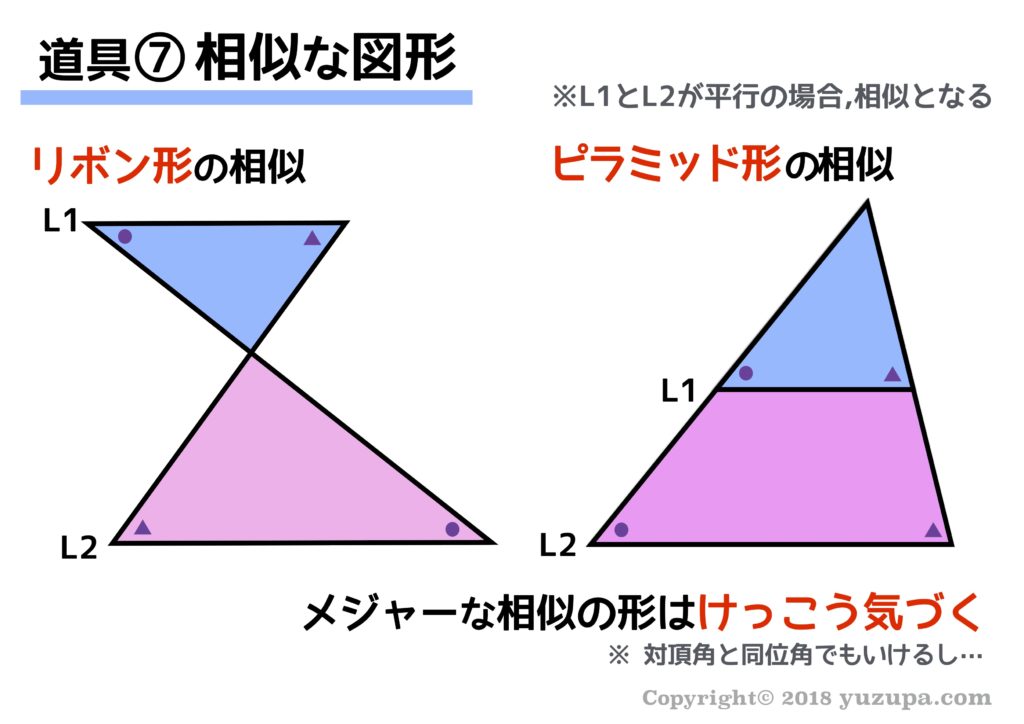



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




解答 オリジナル問題2 2つの辺の長さが同じ三角形 図形問題で柔らか頭に 算数オリピック 中学入試問題にチャレンジ



1




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



正三角形が作る角度 基礎




なつおの部屋 計算ソフト フレーム 6 直角のない三角形の角度計算



二等辺三角形 In 直角三角形 角度の問題 算数の広場




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




ちょうちょ型図形の角度は 求め方を徹底解説 数スタ




底辺が共通な2つの三角形の角度について ある視覚生理系のテキストの 数学 教えて Goo




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




小5 算数 小5 31 三角形の角 Youtube



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
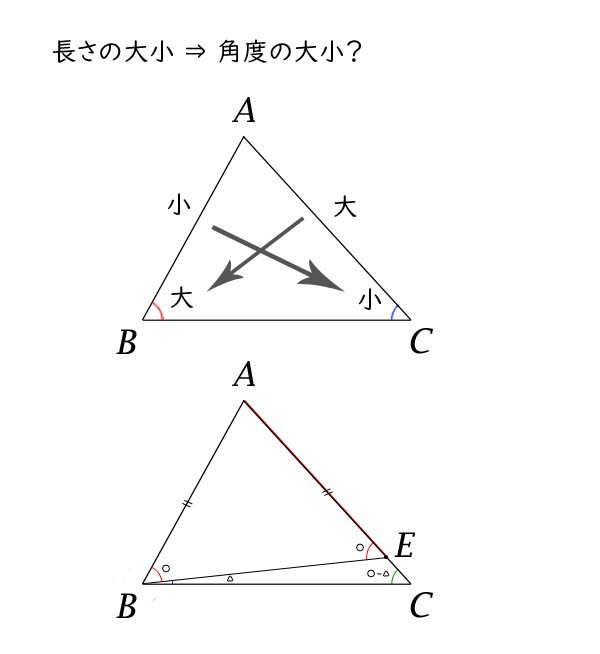



三角形の辺の長さと角の大きさの関係 高校数学マスター




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
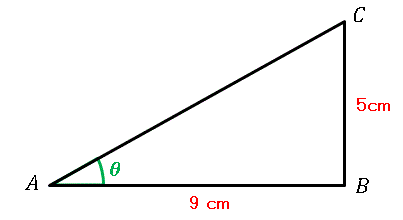



Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます




重なり合う三角定規を使った角度の計算問題 小4 小5の算数 きいとこ
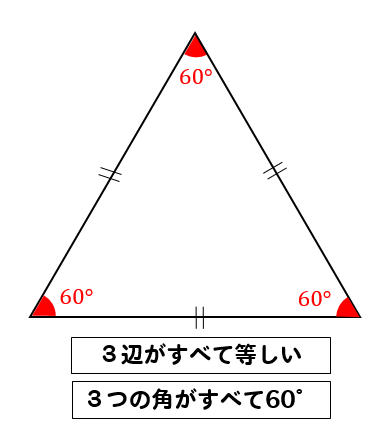



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ



三角形の角度を求める 思考力を鍛える数学




Nikkei Style 算数の問題です 三角形abcの辺bdと辺ecが同じ長さのとき 角abdは何度になるでしょうか この三角形の角度は 算数オリンピックに挑戦 T Co Pjmucyiz5f




二等辺三角形の角を求める Youtube
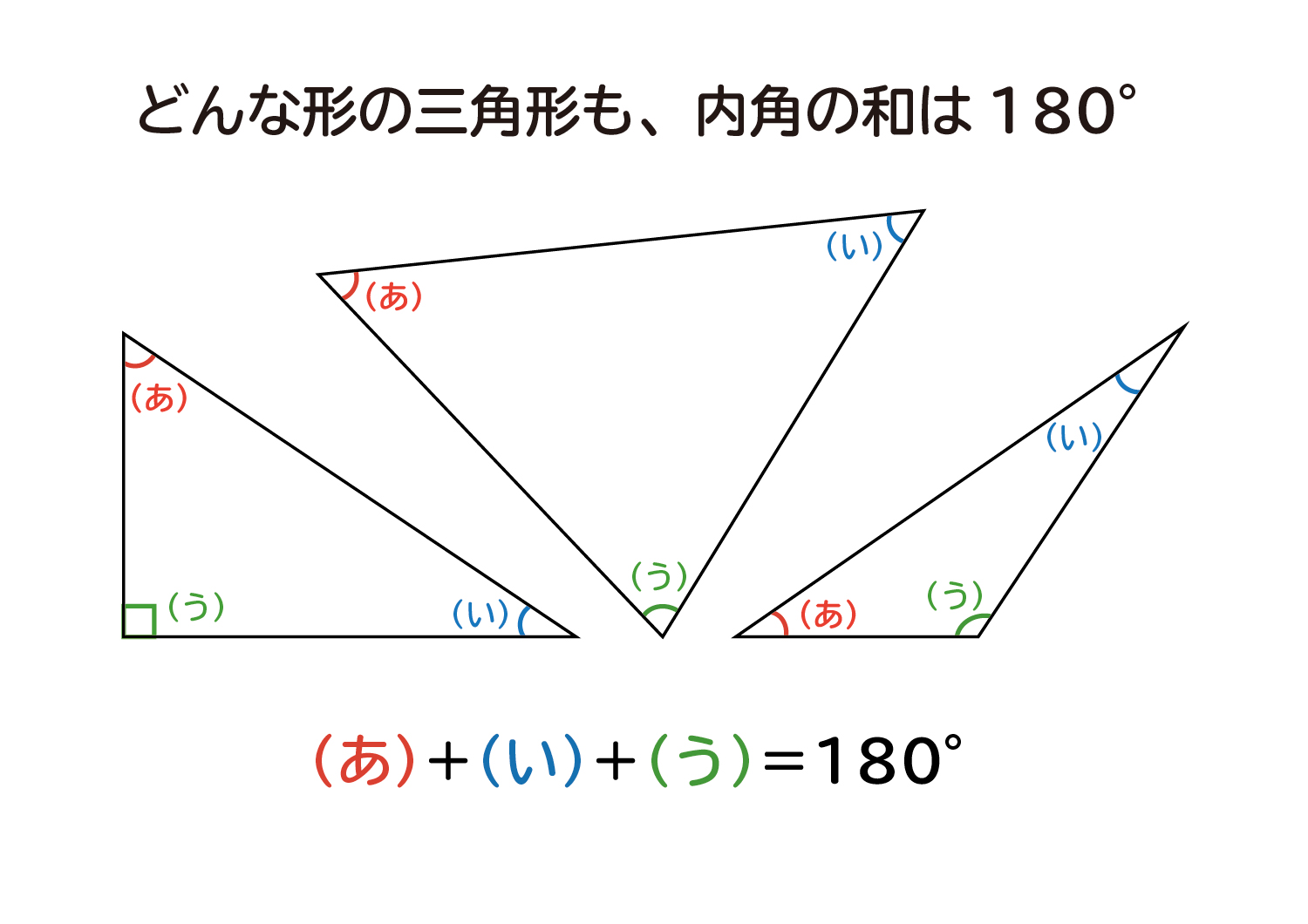



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル




底辺と高さから角度と斜辺を計算 高精度計算サイト




正三角形や二等辺三角形の内角 Youtube




黄金三角形による18 シリーズの三角比 おいしい数学
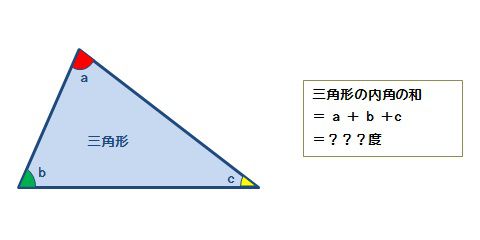



三角形の内角の和 算数の公式覚えてますか




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題
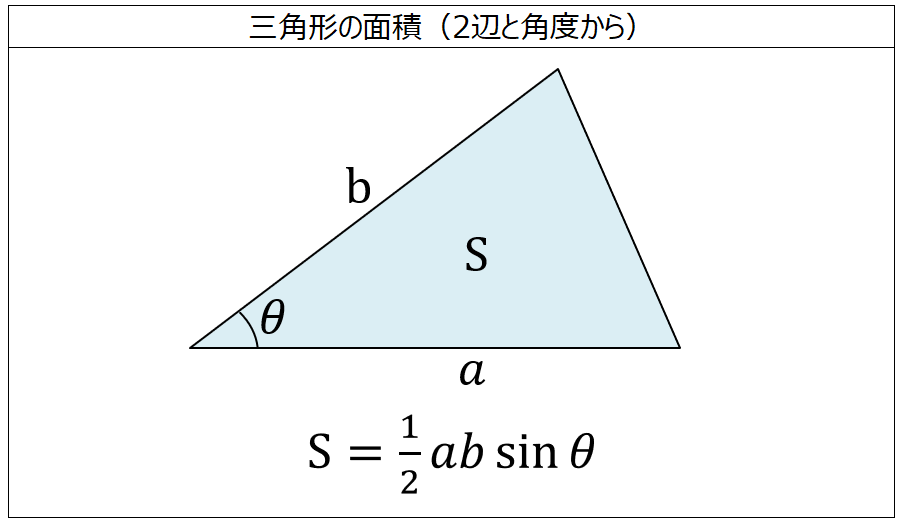



面積の計算 三角形 2辺と角度から 製品設計知識




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




中2 数学 4 2 三角形の角度の利用 Youtube
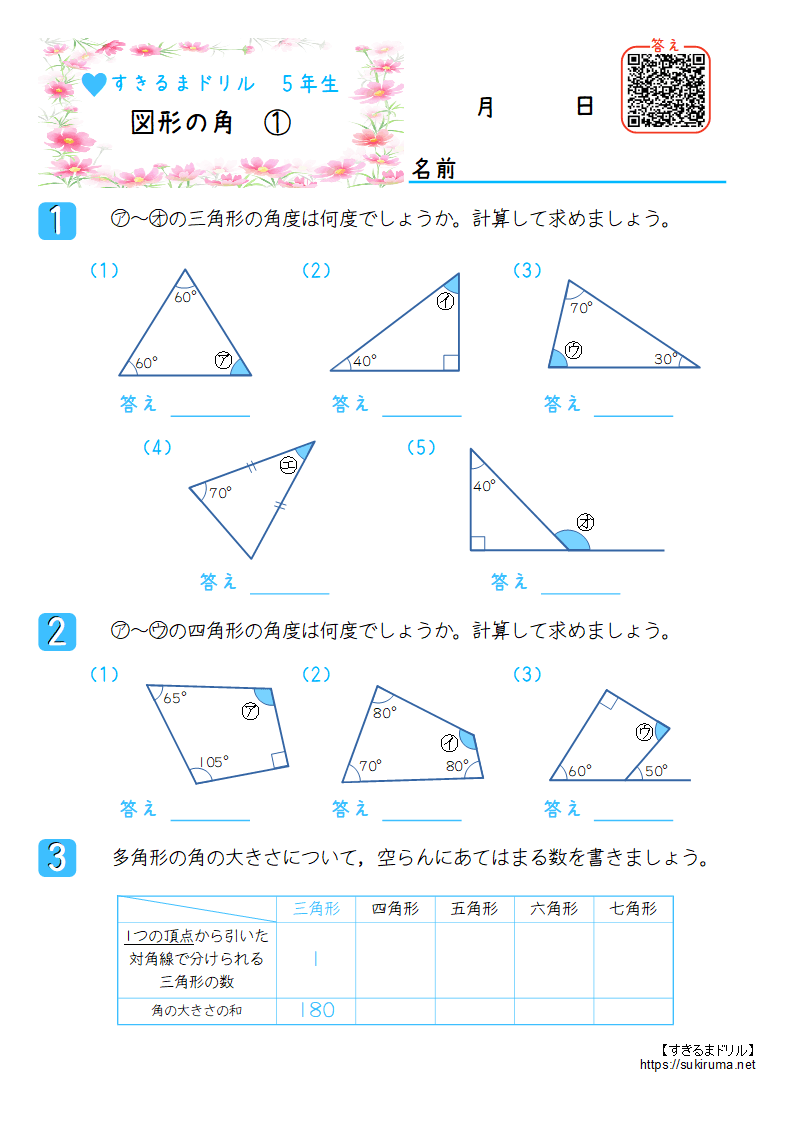



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント




三角定規と角度が 150 の三角形の長さと面積を求める Irohabook




三角形の角度を計算する方法



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




三角形の辺から角度を計算 製品設計知識




角度の求め方 算数の教え上手 学びの場 Com




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun




正三角形の角度問題 シンプルですが面白い 脳トレにはちょうど良い問題です ネタファクト




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
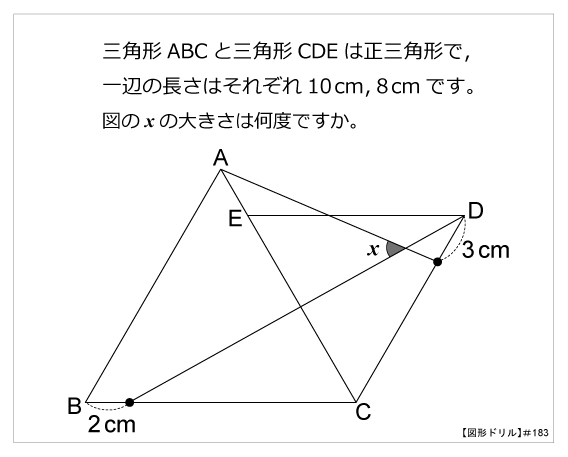



図形ドリル 第1問 正三角形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦




算数 小4 9 角の大きさ 三角じょうぎ Youtube




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット



1
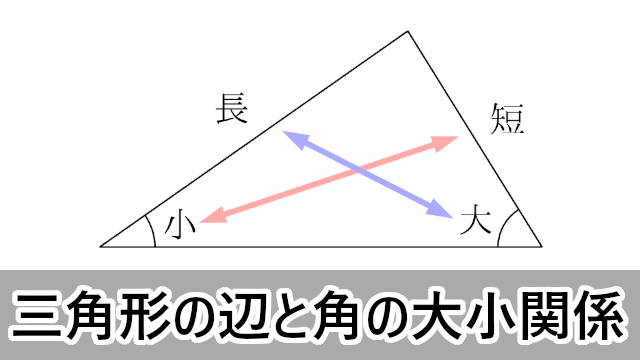



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
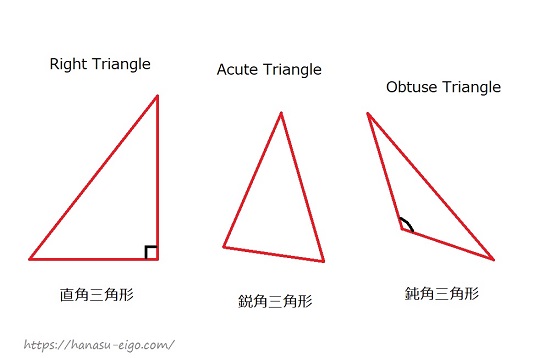



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
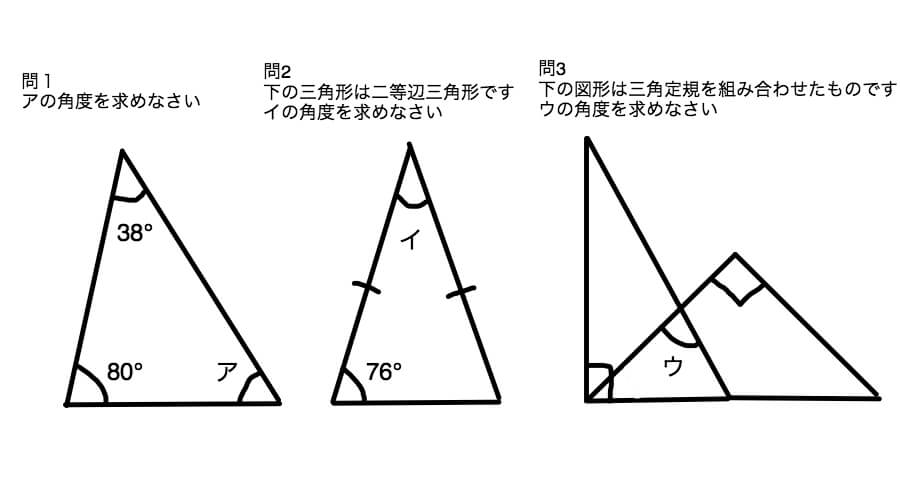



中学受験 小学4年生予習シリーズ算数 第8回 三角形の角 基本知識と解くコツ



1
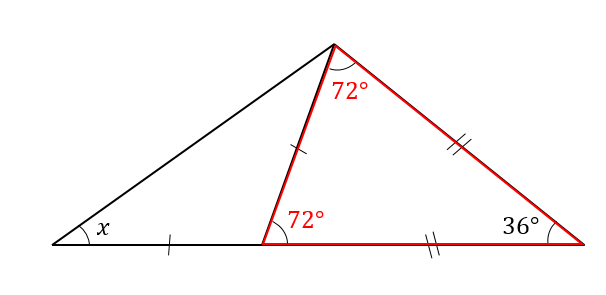



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
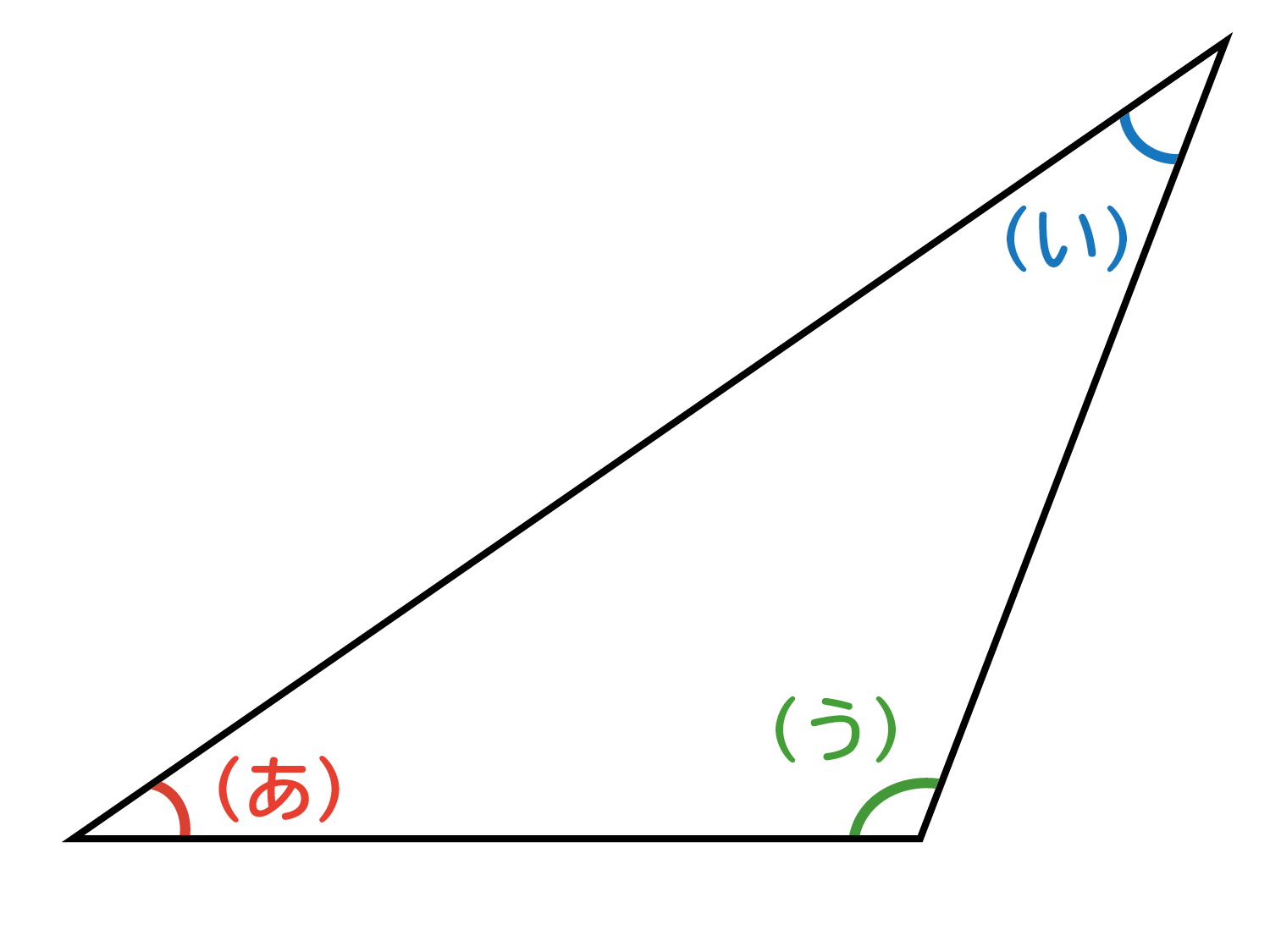



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル




解決済み スケッチにおいての寸法角度の変更について教えて下さい Autodesk Community International Forums




三角形の角度を求める問題 小学生 中学生の勉強



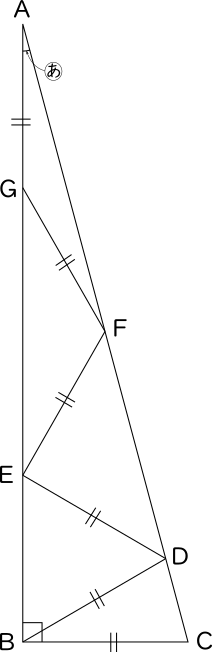
2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に
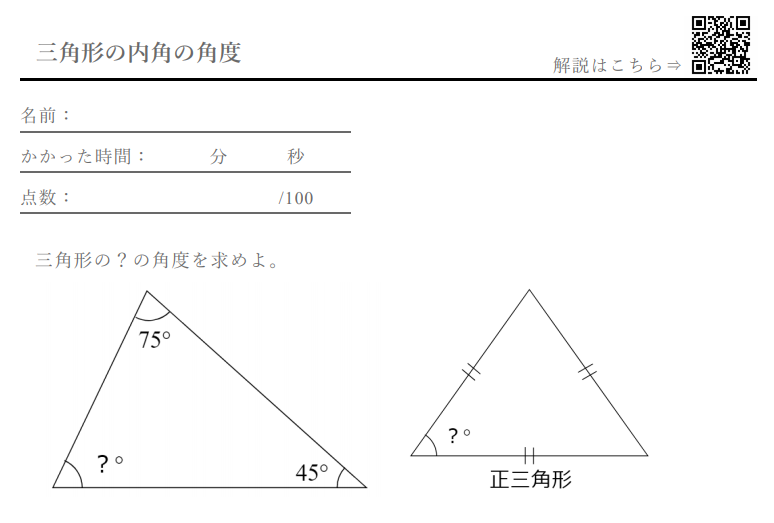



三角形 の内角の角度 計算ドリル 問題集 数学fun




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
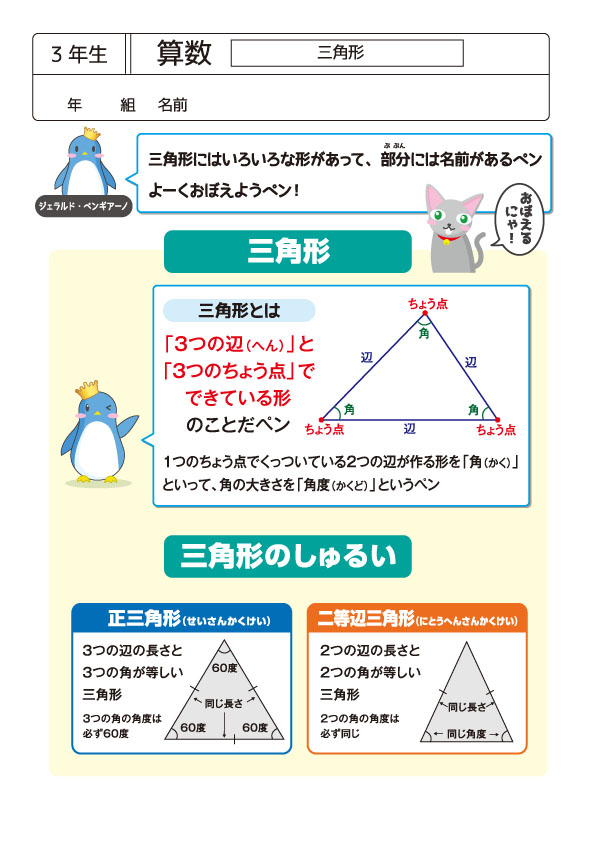



無料の学習プリント 小学3年生の算数 三角形 みそにゃch




三角形の3辺から角度を計算 高精度計算サイト
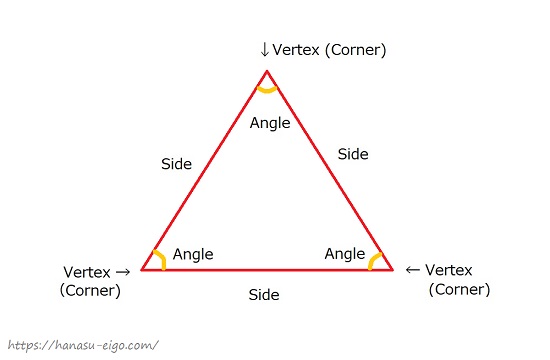



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



3 4 5と1 2 3と3角定規とtvと黄金比と 万象酔歩
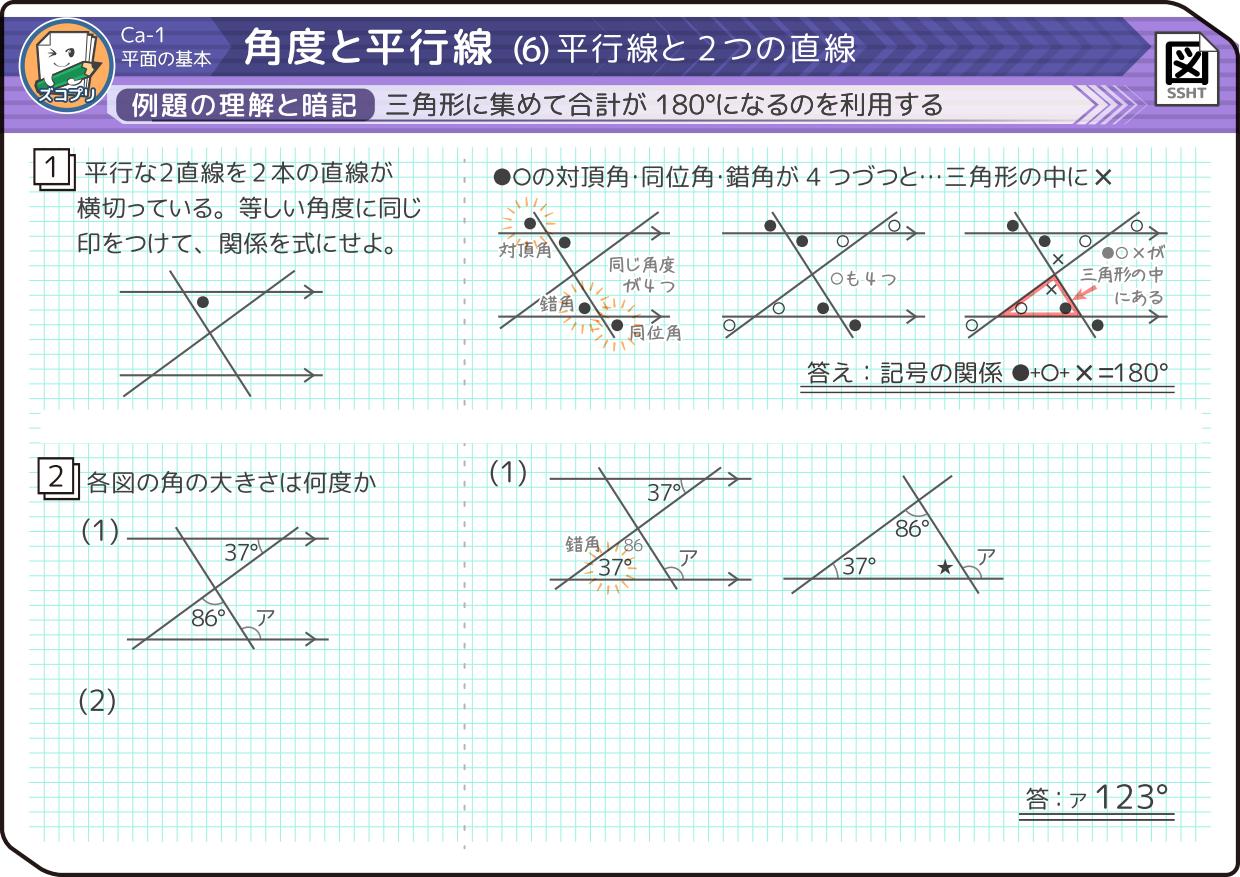



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




余弦定理で角度を求める方法 数学の星
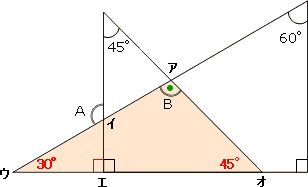



角度の求め方 算数の教え上手 学びの場 Com



Math 平行と合同 角の二等分線と角度 働きアリ




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
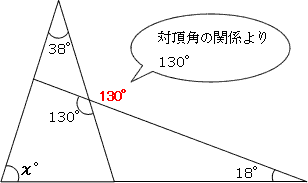



角度の求め方 算数の教え上手 学びの場 Com



Http Sansutp Com A03 05 Pdf
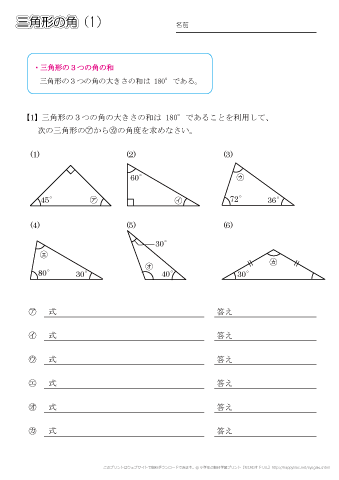



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
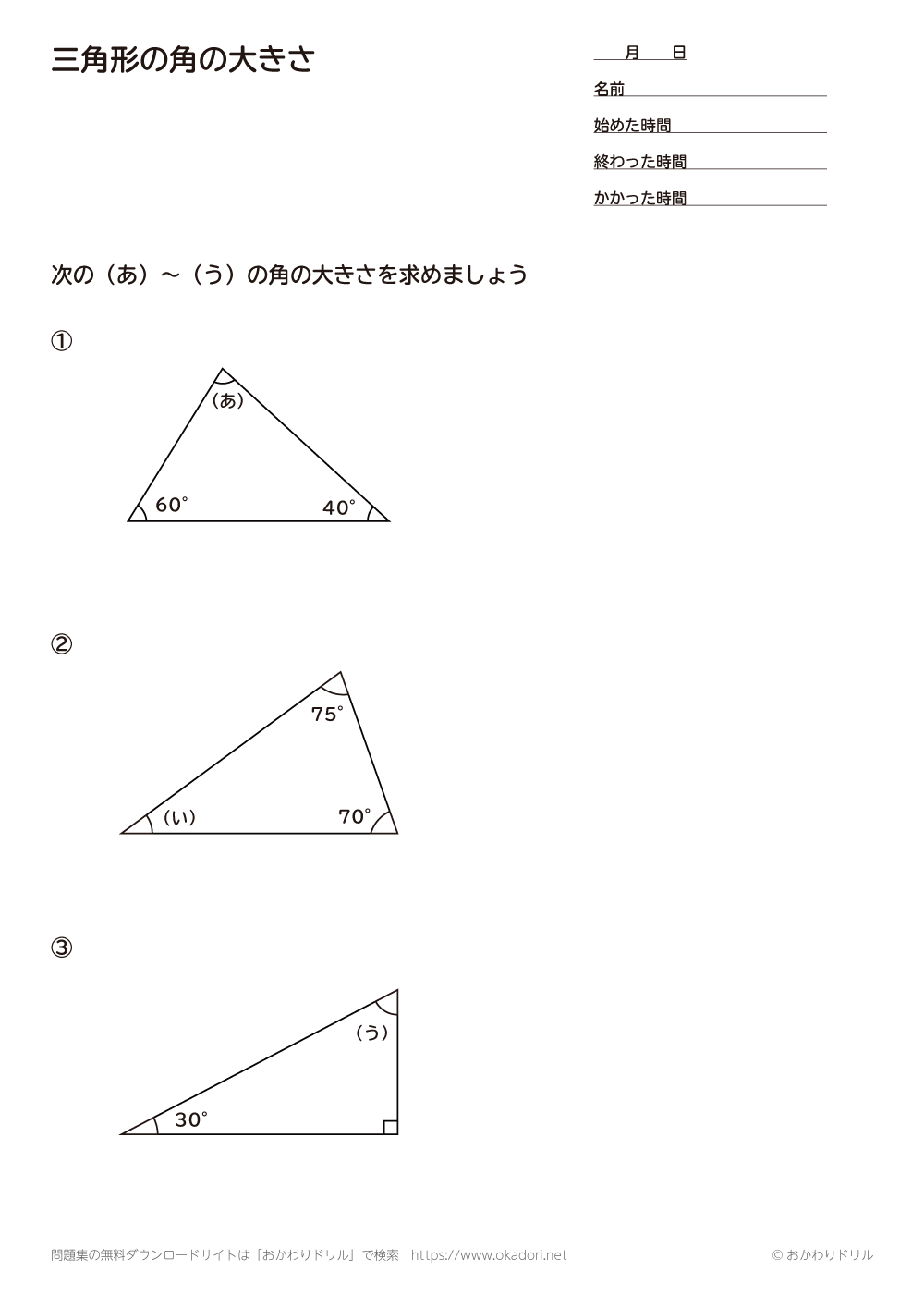



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル



中学生の数学 角度の問題



二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




あ かまでの角度を求めてください 急いでます 教えてください Clear



直角三角形の解法 1



円と三角形 角度 中学から数学だいすき


